Vector Arithmetic
This tutorial covers essential vector arithmetic operations, including addition, subtraction, and multiplication, using SplashKit functions. These operations are fundamental for tasks such as calculating movement, force, and direction in game development and physics simulations.
Written by:
Last updated: 08 Dec 24
While some Python code has been included in basic functions, full Python code for this tutorial is still in development.
Vector Arithmetic
Section titled “Vector Arithmetic”Vector arithmetic involves the addition, subtraction, and multiplication of vectors. These operations are used in various programming scenarios, particularly in game development and physics simulations, to calculate and manipulate directions, positions, and forces.
SplashKit Vector Functions Used in This Tutorial
Section titled “SplashKit Vector Functions Used in This Tutorial”Vector Addition
Section titled “Vector Addition”For example, adding vectors v1 and v2 is computed as:
We can make use of the vector_add function to compute this as follows:
vector_2d v1 = {100, 50};vector_2d v2 = {200, 150};vector_2d result = vector_add(v1, v2);new Vector2D() {((X = 200), (Y = 150))}; Vector2D result =SplashKit.VectorAdd(v1, v2);v1 = Vector2D()v1.x = 100v1.y = 50
v2 = Vector2D()v2.x = 200v2.y = 150
result = vector_add(v1, v2)In this example, v1 and v2 are added together to produce a new vector result with values (300, 200).

Use this code in your own IDE to play with the functions for yourself!
#include "splashkit.h"
using std::to_string;
const int GRID_SPACING = 50;
void draw_cartesian_grid(){ // Draw vertical lines and labels for (int x = 0; x < screen_width(); x += GRID_SPACING) { draw_line(COLOR_LIGHT_GRAY, x, 0, x, screen_height()); if (x != screen_width() / 2) // Avoid overlapping with the y-axis label { draw_text(to_string(x - screen_width() / 2), COLOR_BLACK, x, screen_height() / 2 + 5); } }
// Draw horizontal lines and labels for (int y = 0; y < screen_height(); y += GRID_SPACING) { draw_line(COLOR_LIGHT_GRAY, 0, y, screen_width(), y); if (y != screen_height() / 2) // Avoid overlapping with the x-axis label { draw_text(to_string(screen_height() / 2 - y), COLOR_BLACK, screen_width() / 2 + 5, y); } }
// Draw x-axis and y-axis draw_line(COLOR_BLACK, 0, screen_height() / 2, screen_width(), screen_height() / 2); // x-axis draw_line(COLOR_BLACK, screen_width() / 2, 0, screen_width() / 2, screen_height()); // y-axis
// Label the origin draw_text("0", COLOR_BLACK, screen_width() / 2 + 5, screen_height() / 2 + 5);}
int main(){ open_window("Vector Addition", 800, 600);
// Define vectors vector_2d vector_a; vector_a.x = 100; vector_a.y = 50;
vector_2d vector_b; vector_b.x = 200; vector_b.y = 150;
// Calculate vector addition vector_2d vector_sum = vector_add(vector_a, vector_b);
// Define the origin (centre of the window) point_2d origin; origin.x = 400; origin.y = 300;
// Main loop while (!window_close_requested("Vector Addition")) { process_events(); clear_screen(COLOR_WHITE);
// Draw Cartesian grid draw_cartesian_grid();
// Draw the vectors as lines from the center of the screen draw_line(COLOR_RED, origin.x, origin.y, origin.x + vector_a.x, origin.y - vector_a.y); draw_line(COLOR_GREEN, origin.x, origin.y, origin.x + vector_b.x, origin.y - vector_b.y); draw_line(COLOR_BLUE, origin.x, origin.y, origin.x + vector_sum.x, origin.y - vector_sum.y);
// Display vector properties on the screen draw_text("Vector A (R): " + vector_to_string(vector_a), COLOR_BLACK, 10, 10); draw_text("Vector B (G): " + vector_to_string(vector_b), COLOR_BLACK, 10, 30); draw_text("Sum (B): " + vector_to_string(vector_sum), COLOR_BLACK, 10, 50);
refresh_screen(60); }
return 0;}using System;using SplashKitSDK;
// Constantsconst int GRID_SPACING = 50;
// Function to draw the Cartesian gridvoid DrawCartesianGrid(){// Draw vertical lines and labelsfor (int x = 0; x < SplashKit.ScreenWidth(); x += GRID_SPACING){SplashKit.DrawLine(Color.LightGray, x, 0, x, SplashKit.ScreenHeight());if (x != SplashKit.ScreenWidth() / 2) // Avoid overlapping with the y-axis label{SplashKit.DrawText((x - SplashKit.ScreenWidth() / 2).ToString(), Color.Black, x, SplashKit.ScreenHeight() / 2 + 5);}}
// Draw horizontal lines and labels for (int y = 0; y < SplashKit.ScreenHeight(); y += GRID_SPACING) { SplashKit.DrawLine(Color.LightGray, 0, y, SplashKit.ScreenWidth(), y); if (y != SplashKit.ScreenHeight() / 2) // Avoid overlapping with the x-axis label { SplashKit.DrawText((SplashKit.ScreenHeight() / 2 - y).ToString(), Color.Black, SplashKit.ScreenWidth() / 2 + 5, y); } }
// Draw x-axis and y-axis SplashKit.DrawLine(Color.Black, 0, SplashKit.ScreenHeight() / 2, SplashKit.ScreenWidth(), SplashKit.ScreenHeight() / 2); // x-axis SplashKit.DrawLine(Color.Black, SplashKit.ScreenWidth() / 2, 0, SplashKit.ScreenWidth() / 2, SplashKit.ScreenHeight()); // y-axis
// Label the origin SplashKit.DrawText("0", Color.Black, SplashKit.ScreenWidth() / 2 + 5, SplashKit.ScreenHeight() / 2 + 5);
}
// Main program logic using top-level statementsSplashKit.OpenWindow("Vector Addition", 800, 600);
// Define vectorsVector2D vectorA = new Vector2D() { X = 100, Y = 50 };Vector2D vectorB = new Vector2D() { X = 200, Y = 150 };
// Calculate vector additionVector2D vectorSum = SplashKit.VectorAdd(vectorA, vectorB);
// Define the origin (center of the window)Point2D origin = new Point2D() { X = 400, Y = 300 };
// Main loopwhile (!SplashKit.WindowCloseRequested("Vector Addition")){ SplashKit.ProcessEvents(); SplashKit.ClearScreen(Color.White);
// Draw Cartesian grid DrawCartesianGrid();
// Draw the vectors as lines from the center of the screen SplashKit.DrawLine(Color.Red, origin.X, origin.Y, origin.X + vectorA.X, origin.Y - vectorA.Y); SplashKit.DrawLine(Color.Green, origin.X, origin.Y, origin.X + vectorB.X, origin.Y - vectorB.Y); SplashKit.DrawLine(Color.Blue, origin.X, origin.Y, origin.X + vectorSum.X, origin.Y - vectorSum.Y);
// Display vector properties on the screen SplashKit.DrawText("Vector A (R): " + SplashKit.VectorToString(vectorA), Color.Black, 10, 10); SplashKit.DrawText("Vector B (G): " + SplashKit.VectorToString(vectorB), Color.Black, 10, 30); SplashKit.DrawText("Sum (B): " + SplashKit.VectorToString(vectorSum), Color.Black, 10, 50);
SplashKit.RefreshScreen(60);}Vector Subtraction
Section titled “Vector Subtraction”For example, subtracting vector v2 from v1 gives:
We can make use of the vector_subtract function to compute this as follows:
vector_2d v1 = {300, 200};vector_2d v2 = {100, 50};vector_2d result = vector_subtract(v1, v2);new Vector2D() {((X = 100), (Y = 50))}; Vector2D result =SplashKit.VectorSubtract(v1, v2);v1 = Vector2D()v1.x = 300v1.y = 200
v2 = Vector2D()v2.x = 2100v2.y = 50
result = vector_subtract(v1, v2)In this example, v2 is subtracted from v1 to produce a new vector result with values (200, 150).
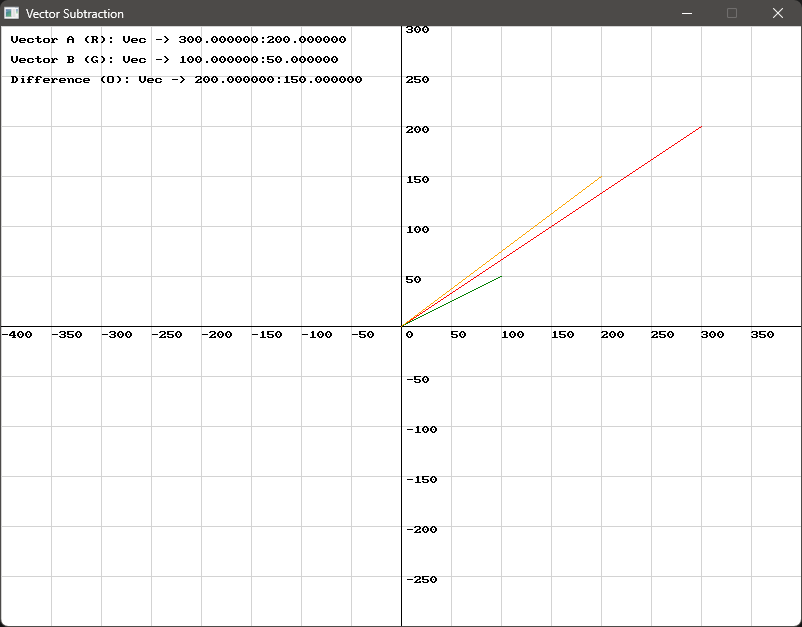
Use this code in your own IDE to play with the functions for yourself!
#include "splashkit.h"
using std::to_string;
const int GRID_SPACING = 50;
void draw_cartesian_grid(){ // Draw vertical lines and labels for (int x = 0; x < screen_width(); x += GRID_SPACING) { draw_line(COLOR_LIGHT_GRAY, x, 0, x, screen_height()); if (x != screen_width() / 2) // Avoid overlapping with the y-axis label { draw_text(to_string(x - screen_width() / 2), COLOR_BLACK, x, screen_height() / 2 + 5); } }
// Draw horizontal lines and labels for (int y = 0; y < screen_height(); y += GRID_SPACING) { draw_line(COLOR_LIGHT_GRAY, 0, y, screen_width(), y); if (y != screen_height() / 2) // Avoid overlapping with the x-axis label { draw_text(to_string(screen_height() / 2 - y), COLOR_BLACK, screen_width() / 2 + 5, y); } }
// Draw x-axis and y-axis draw_line(COLOR_BLACK, 0, screen_height() / 2, screen_width(), screen_height() / 2); // x-axis draw_line(COLOR_BLACK, screen_width() / 2, 0, screen_width() / 2, screen_height()); // y-axis
// Label the origin draw_text("0", COLOR_BLACK, screen_width() / 2 + 5, screen_height() / 2 + 5);}
int main(){ open_window("Vector Subtraction", 800, 600);
// Define vectors vector_2d vector_a; vector_a.x = 300; vector_a.y = 200;
vector_2d vector_b; vector_b.x = 100; vector_b.y = 50;
// Calculate vector subtraction vector_2d vector_difference = vector_subtract(vector_a, vector_b);
// Define the origin (centre of the window) point_2d origin; origin.x = 400; origin.y = 300;
// Main loop while (!window_close_requested("Vector Subtraction")) { process_events(); clear_screen(COLOR_WHITE);
// Draw Cartesian grid draw_cartesian_grid();
// Draw the vectors as lines from the center of the screen draw_line(COLOR_RED, origin.x, origin.y, origin.x + vector_a.x, origin.y - vector_a.y); draw_line(COLOR_GREEN, origin.x, origin.y, origin.x + vector_b.x, origin.y - vector_b.y); draw_line(COLOR_ORANGE, origin.x, origin.y, origin.x + vector_difference.x, origin.y - vector_difference.y);
// Display vector properties on the screen draw_text("Vector A (R): " + vector_to_string(vector_a), COLOR_BLACK, 10, 10); draw_text("Vector B (G): " + vector_to_string(vector_b), COLOR_BLACK, 10, 30); draw_text("Difference (O): " + vector_to_string(vector_difference), COLOR_BLACK, 10, 50);
refresh_screen(60); }
return 0;}using System;using SplashKitSDK;
// Constantsconst int GRID_SPACING = 50;
// Function to draw the Cartesian gridvoid DrawCartesianGrid(){ // Draw vertical lines and labels for (int x = 0; x < SplashKit.ScreenWidth(); x += GRID_SPACING) { SplashKit.DrawLine(Color.LightGray, x, 0, x, SplashKit.ScreenHeight()); if (x != SplashKit.ScreenWidth() / 2) // Avoid overlapping with the y-axis label { SplashKit.DrawText((x - SplashKit.ScreenWidth() / 2).ToString(), Color.Black, x, SplashKit.ScreenHeight() / 2 + 5); } }
// Draw horizontal lines and labels for (int y = 0; y < SplashKit.ScreenHeight(); y += GRID_SPACING) { SplashKit.DrawLine(Color.LightGray, 0, y, SplashKit.ScreenWidth(), y); if (y != SplashKit.ScreenHeight() / 2) // Avoid overlapping with the x-axis label { SplashKit.DrawText((SplashKit.ScreenHeight() / 2 - y).ToString(), Color.Black, SplashKit.ScreenWidth() / 2 + 5, y); } }
// Draw x-axis and y-axis SplashKit.DrawLine(Color.Black, 0, SplashKit.ScreenHeight() / 2, SplashKit.ScreenWidth(), SplashKit.ScreenHeight() / 2); // x-axis SplashKit.DrawLine(Color.Black, SplashKit.ScreenWidth() / 2, 0, SplashKit.ScreenWidth() / 2, SplashKit.ScreenHeight()); // y-axis
// Label the origin SplashKit.DrawText("0", Color.Black, SplashKit.ScreenWidth() / 2 + 5, SplashKit.ScreenHeight() / 2 + 5);}
// Main program logic using top-level statementsSplashKit.OpenWindow("Vector Subtraction", 800, 600);
// Define vectorsVector2D vectorA = new Vector2D() { X = 300, Y = 200 };Vector2D vectorB = new Vector2D() { X = 100, Y = 50 };
// Calculate vector subtractionVector2D vectorDifference = SplashKit.VectorSubtract(vectorA, vectorB);
// Define the origin (center of the window)Point2D origin = new Point2D() { X = 400, Y = 300 };
// Main loopwhile (!SplashKit.WindowCloseRequested("Vector Subtraction")){ SplashKit.ProcessEvents(); SplashKit.ClearScreen(Color.White);
// Draw Cartesian grid DrawCartesianGrid();
// Draw the vectors as lines from the center of the screen SplashKit.DrawLine(Color.Red, origin.X, origin.Y, origin.X + vectorA.X, origin.Y - vectorA.Y); SplashKit.DrawLine(Color.Green, origin.X, origin.Y, origin.X + vectorB.X, origin.Y - vectorB.Y); SplashKit.DrawLine(Color.Orange, origin.X, origin.Y, origin.X + vectorDifference.X, origin.Y - vectorDifference.Y);
// Display vector properties on the screen SplashKit.DrawText("Vector A (R): " + SplashKit.VectorToString(vectorA), Color.Black, 10, 10); SplashKit.DrawText("Vector B (G): " + SplashKit.VectorToString(vectorB), Color.Black, 10, 30); SplashKit.DrawText("Difference (O): " + SplashKit.VectorToString(vectorDifference), Color.Black, 10, 50);
SplashKit.RefreshScreen(60);}Practical Applications of Vector Addition and Subtraction
Section titled “Practical Applications of Vector Addition and Subtraction”Vector addition and subtraction are fundamental operations in game development, particularly in handling movement, physics, and collision detection. For example, when simulating a character’s movement in a game, multiple forces like gravity, wind, or user input can be combined using vector addition to determine the character’s final trajectory. Similarly, vector subtraction can be used to calculate the relative velocity between two objects, such as a missile and a target, helping in predicting collisions or adjusting aiming mechanics.
Scenario: Character Movement with Multiple Forces
Section titled “Scenario: Character Movement with Multiple Forces”In a platform game, a character is affected by multiple forces: user input (e.g., moving left or right), gravity, and wind.
Each of these forces can be represented as vectors:
- User Input Vector: Represents the direction and speed of movement based on player input (e.g., moving right might be
(3, 0)). - Gravity Vector: Acts downwards, pulling the character down (e.g.,
(0, -9.8)). - Wind Vector: Blows horizontally, affecting the character’s movement (e.g.,
(-2, 0)if it’s blowing left).
By adding these vectors, you get the character’s final movement vector:
vector_2d user_input = {35, 0}; // Moving rightvector_2d gravity = {0, -9.8}; // Gravity pulling downvector_2d wind = {-20, 0}; // Wind blowing left
vector_2d final_movement = vector_add(vector_add(user_input, gravity), wind); // Combining all forcesVector2D userInput = new Vector2D() { X = 35, Y = 0 }; // Moving rightVector2D gravity = new Vector2D() { X = 0, Y = -9.8 }; // Gravity pulling downVector2D wind = new Vector2D() { X = -20, Y = 0 }; // Wind blowing left
Vector2D finalMovement = SplashKit.VectorAdd(SplashKit.VectorAdd(userInput, gravity), wind);Let’s visualise this!
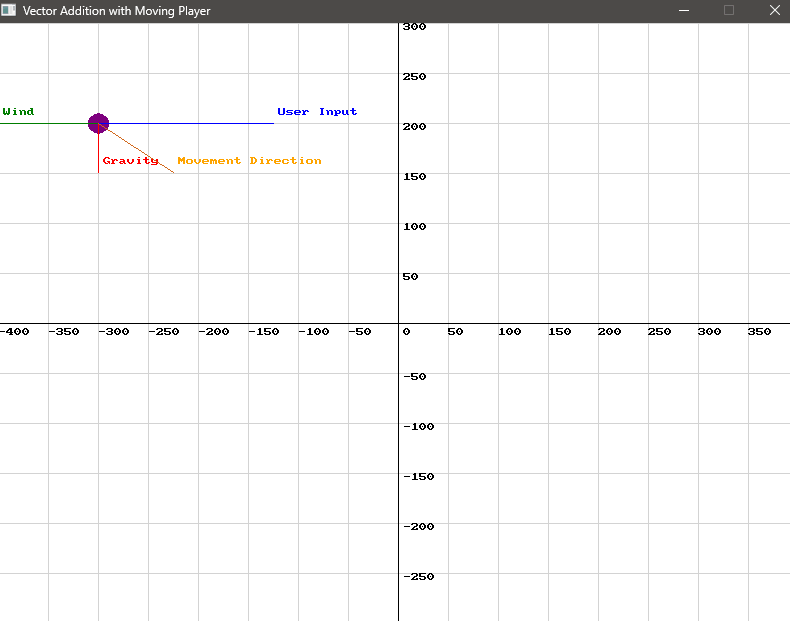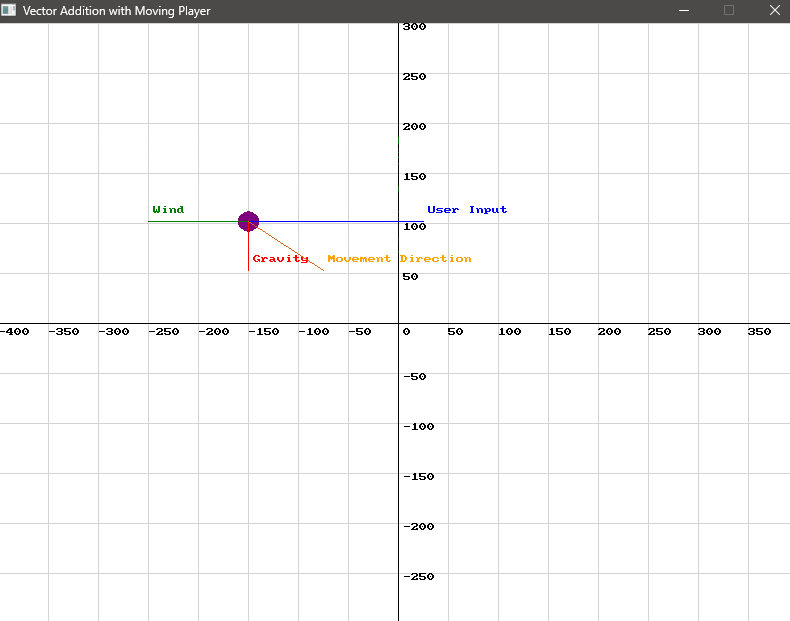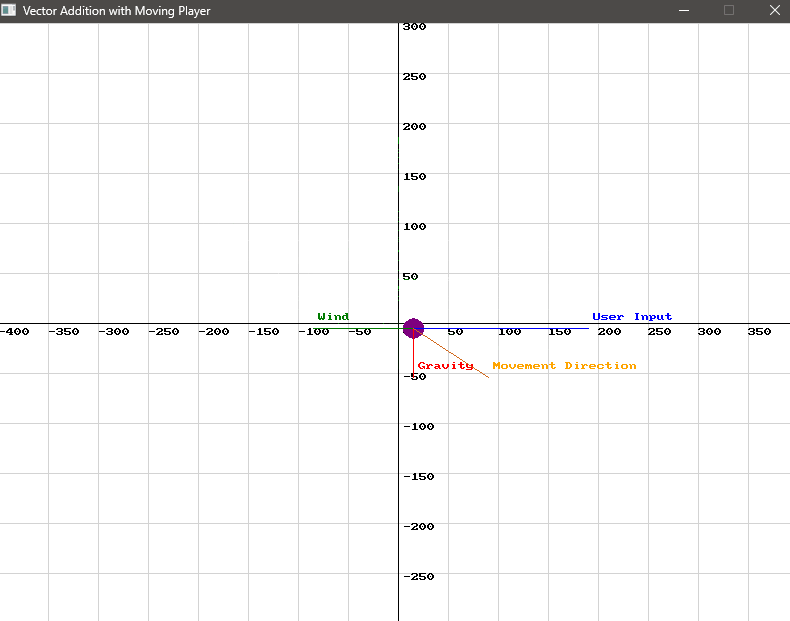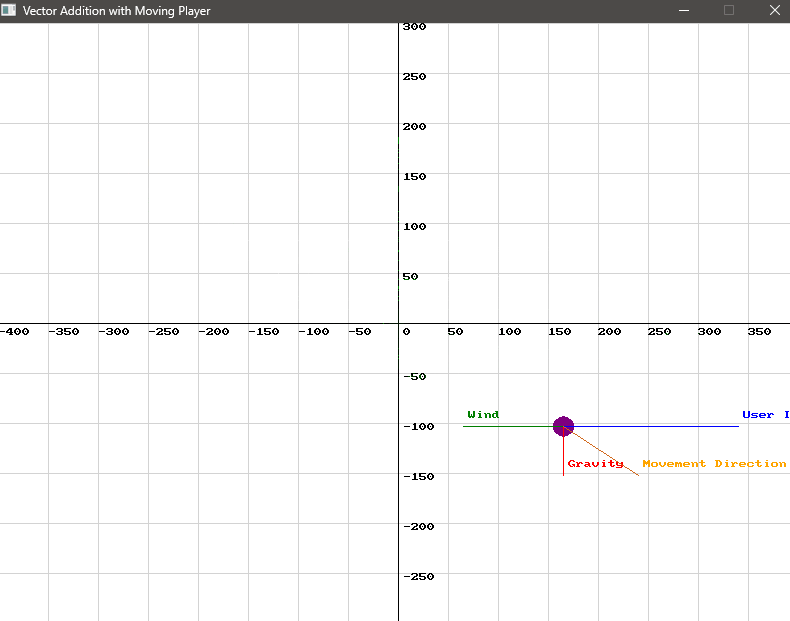
Use this code in your own IDE to play with the functions for yourself!
#include "splashkit.h"
using std::to_string;
const int GRID_SPACING = 50; // Define grid spacing for the Cartesian grid
// Function to draw a vector on the screenvoid draw_vector(vector_2d vec, color c, point_2d start_point, string label, double scale){ point_2d end_point = {start_point.x + vec.x_ scale, start_point.y - vec.y_ scale}; // Adjust scale as needed draw_line(c, start_point.x, start_point.y, end_point.x, end_point.y); draw_text(label, c, end_point.x + 5, end_point.y - 15); // Adjust text position to avoid overlap}
// Function to draw the Cartesian gridvoid draw_cartesian_grid(){ // Draw vertical lines and labels for (int x = 0; x < screen_width(); x += GRID_SPACING) { draw_line(COLOR_LIGHT_GRAY, x, 0, x, screen_height()); if (x != screen_width() / 2) // Avoid overlapping with the y-axis label { draw_text(to_string(x - screen_width() / 2), COLOR_BLACK, x, screen_height() / 2 + 5); } }
// Draw horizontal lines and labels for (int y = 0; y < screen_height(); y += GRID_SPACING) { draw_line(COLOR_LIGHT_GRAY, 0, y, screen_width(), y); if (y != screen_height() / 2) // Avoid overlapping with the x-axis label { draw_text(to_string(screen_height() / 2 - y), COLOR_BLACK, screen_width() / 2 + 5, y); } }
// Draw x-axis and y-axis draw_line(COLOR_BLACK, 0, screen_height() / 2, screen_width(), screen_height() / 2); // x-axis draw_line(COLOR_BLACK, screen_width() / 2, 0, screen_width() / 2, screen_height()); // y-axis
// Label the origin draw_text("0", COLOR_BLACK, screen_width() / 2 + 5, screen_height() / 2 + 5);}
int main(){// Set up the windowopen_window("Vector Addition with Moving Player", 800, 600);
// Initial position of the player (starting at 100, 100) point_2d player_pos = {100, 100}; point_2d initial_pos = player_pos; // Store the initial position for final vector
// Define the vectors vector_2d user_input = {35, 0}; // Moving right vector_2d gravity = {0, -9.8}; // Gravity pulling down vector_2d wind = {-20, 0}; // Wind blowing left
// Calculate the final movement vector vector_2d final_movement = vector_add(vector_add(user_input, gravity), wind);
while (!window_close_requested("Vector Addition with Moving Player")) { // Process events process_events();
// Clear the screen clear_screen(COLOR_WHITE);
// Draw the Cartesian grid draw_cartesian_grid();
// Draw the player (a circle) at the current position fill_circle(COLOR_PURPLE, player_pos.x, player_pos.y, 10);
// Draw the individual vectors acting on the player // Scale factor adjusted to make vectors visible double scale_factor = 5; // Adjust as needed
// Draw user input vector draw_vector(user_input, COLOR_BLUE, player_pos, "User Input", scale_factor);
// Draw gravity vector point_2d gravity_end = {player_pos.x, player_pos.y - gravity.y * scale_factor}; // Gravity vector should extend downwards draw_line(COLOR_RED, player_pos.x, player_pos.y, gravity_end.x, gravity_end.y); draw_text("Gravity", COLOR_RED, gravity_end.x + 5, gravity_end.y - 15); // Adjust text position to avoid overlap
// Draw wind vector point_2d wind_end = {player_pos.x + wind.x * scale_factor, player_pos.y}; // Wind vector should extend horizontally to the left draw_line(COLOR_GREEN, player_pos.x, player_pos.y, wind_end.x, wind_end.y); draw_text("Wind", COLOR_GREEN, wind_end.x + 5, wind_end.y - 15); // Adjust text position to avoid overlap
// Draw the final movement vector from the initial position to the current position point_2d final_movement_end = {player_pos.x + final_movement.x * scale_factor, player_pos.y - final_movement.y * scale_factor}; draw_line(COLOR_CHOCOLATE, player_pos.x, player_pos.y, final_movement_end.x, final_movement_end.y); draw_text("Movement Direction", COLOR_ORANGE, final_movement_end.x + 5, final_movement_end.y - 15); // Adjust text position to avoid overlap
// Update the player's position based on the final movement vector player_pos.x += final_movement.x; player_pos.y -= final_movement.y; // Inverted Y because of screen coordinates
// Add delay to assist visualisation delay(250);
// Refresh the screen refresh_screen(60); } return 0;}using System;using SplashKitSDK;
const int GRID_SPACING = 50; // Define grid spacing for the Cartesian grid
// Function to draw a vector on the screenvoid DrawVector(Vector2D vec, Color c, Point2D startPoint, string label, double scale){ Point2D endPoint = new Point2D { X = startPoint.X + vec.X *scale, Y = startPoint.Y - vec.Y* scale }; // Adjust scale as needed
SplashKit.DrawLine(c, startPoint.X, startPoint.Y, endPoint.X, endPoint.Y); SplashKit.DrawText(label, c, endPoint.X + 5, endPoint.Y - 15); // Adjust text position to avoid overlap}
// Function to draw the Cartesian gridvoid DrawCartesianGrid(){ // Draw vertical lines and labels for (int x = 0; x < SplashKit.ScreenWidth(); x += GRID_SPACING) { SplashKit.DrawLine(Color.LightGray, x, 0, x, SplashKit.ScreenHeight()); if (x != SplashKit.ScreenWidth() / 2) // Avoid overlapping with the y-axis label { SplashKit.DrawText((x - SplashKit.ScreenWidth() / 2).ToString(), Color.Black, x, SplashKit.ScreenHeight() / 2 + 5); } }
// Draw horizontal lines and labels for (int y = 0; y < SplashKit.ScreenHeight(); y += GRID_SPACING) { SplashKit.DrawLine(Color.LightGray, 0, y, SplashKit.ScreenWidth(), y); if (y != SplashKit.ScreenHeight() / 2) // Avoid overlapping with the x-axis label { SplashKit.DrawText((SplashKit.ScreenHeight() / 2 - y).ToString(), Color.Black, SplashKit.ScreenWidth() / 2 + 5, y); } }
// Draw x-axis and y-axis SplashKit.DrawLine(Color.Black, 0, SplashKit.ScreenHeight() / 2, SplashKit.ScreenWidth(), SplashKit.ScreenHeight() / 2); // x-axis SplashKit.DrawLine(Color.Black, SplashKit.ScreenWidth() / 2, 0, SplashKit.ScreenWidth() / 2, SplashKit.ScreenHeight()); // y-axis
// Label the origin SplashKit.DrawText("0", Color.Black, SplashKit.ScreenWidth() / 2 + 5, SplashKit.ScreenHeight() / 2 + 5);}
// Main program executionWindow window = SplashKit.OpenWindow("Vector Addition with Moving Player", 800, 600);
// Initial position of the player (starting at 100, 100)Point2D playerPos = new Point2D { X = 100, Y = 100 };
// Define the vectorsVector2D userInput = new Vector2D { X = 35, Y = 0 }; // Moving rightVector2D gravity = new Vector2D { X = 0, Y = -9.8 }; // Gravity pulling downVector2D wind = new Vector2D { X = -20, Y = 0 }; // Wind blowing left
// Calculate the final movement vectorVector2D finalMovement = SplashKit.VectorAdd(SplashKit.VectorAdd(userInput, gravity), wind);
while (!SplashKit.WindowCloseRequested("Vector Addition with Moving Player")){ // Process events SplashKit.ProcessEvents();
// Clear the screen SplashKit.ClearScreen(Color.White);
// Draw the Cartesian grid DrawCartesianGrid();
// Draw the player (a circle) at the current position SplashKit.FillCircle(Color.Purple, playerPos.X, playerPos.Y, 10);
// Draw the individual vectors acting on the player double scaleFactor = 5; // Adjust as needed
// Draw user input vector DrawVector(userInput, Color.Blue, playerPos, "User Input", scaleFactor);
// Draw gravity vector Point2D gravityEnd = new Point2D { X = playerPos.X, Y = playerPos.Y - gravity.Y * scaleFactor }; // Gravity vector should extend downwards SplashKit.DrawLine(Color.Red, playerPos.X, playerPos.Y, gravityEnd.X, gravityEnd.Y); SplashKit.DrawText("Gravity", Color.Red, gravityEnd.X + 5, gravityEnd.Y - 15); // Adjust text position to avoid overlap
// Draw wind vector Point2D windEnd = new Point2D { X = playerPos.X + wind.X * scaleFactor, Y = playerPos.Y }; // Wind vector should extend horizontally to the left SplashKit.DrawLine(Color.Green, playerPos.X, playerPos.Y, windEnd.X, windEnd.Y); SplashKit.DrawText("Wind", Color.Green, windEnd.X + 5, windEnd.Y - 15); // Adjust text position to avoid overlap
// Draw the final movement vector from the initial position to the current position Point2D finalMovementEnd = new Point2D { X = playerPos.X + finalMovement.X * scaleFactor, Y = playerPos.Y - finalMovement.Y * scaleFactor }; SplashKit.DrawLine(Color.Chocolate, playerPos.X, playerPos.Y, finalMovementEnd.X, finalMovementEnd.Y); SplashKit.DrawText("Movement Direction", Color.Orange, finalMovementEnd.X + 5, finalMovementEnd.Y - 15); // Adjust text position to avoid overlap
// Update the player's position based on the final movement vector playerPos.X += finalMovement.X; playerPos.Y -= finalMovement.Y; // Inverted Y because of screen coordinates
// Add delay to assist visualization SplashKit.Delay(250);
// Refresh the screen SplashKit.RefreshScreen(60);}Scenario: Calculating Ship Trajectory
Section titled “Scenario: Calculating Ship Trajectory”In a navigation simulation game, a ship is moving towards an island, but it has to account for a current that affects its path. You need to calculate the correct heading for the ship to reach the island directly, considering the current’s influence.
- Ship’s Velocity Vector: Represents the ship’s intended direction and speed.
- Current’s Velocity Vector: Represents the current’s direction and speed affecting the ship’s path.
- Target Vector: Represents the direct line from the ship’s current position to the island.
The goal is to determine the required heading for the ship to counteract the current and head directly to the island.
point_2d ship_position = {-50, 50}; // Ship starts at (-50, 50)point_2d island_position = {200, 250}; // Island at (200, 250)
// Calculate vectorsvector_2d current_vector = {100, 5}; // Current affecting the shipvector_2d target_vector = vector_point_to_point(ship_position, island_position);vector_2d required_vector = vector_subtract(target_vector, current_vector);Point2D shipPosition = new Point2D { X = -50, Y = 50 }; // Ship starts at (-50, 50)Point2D islandPosition = new Point2D { X = 200, Y = 250 }; // Island at (200, 250)
// Calculate vectorsVector2D currentVector = new Vector2D { X = 100, Y = 5 }; // Current affecting the shipVector2D targetVector = SplashKit.VectorPointToPoint(shipPosition, islandPosition);Vector2D requiredVector = SplashKit.VectorSubtract(targetVector, currentVector);Using the vector_subtract function from SplashKit, the required_vector is calculated by subtracting the current_vector from the target_vector. This required_vector represents the direction the ship needs to steer in order to reach the island while counteracting the current.

Use this code in your own IDE to play with the functions for yourself!
#include "splashkit.h"#include "string"
using std::to_string;
// Define constantsconst int GRID_SPACING = 50;
// Function to draw the Cartesian gridvoid draw_cartesian_grid(){ int width = screen_width(); int height = screen_height(); int center_x = width / 2; int center_y = height / 2;
for (int x = 0; x <= width; x += GRID_SPACING) { draw_line(COLOR_LIGHT_GRAY, x, 0, x, height); if (x != center_x) { draw_text(to_string((x - center_x) / GRID_SPACING), COLOR_BLACK, x + 2, center_y + 5); } }
for (int y = 0; y <= height; y += GRID_SPACING) { draw_line(COLOR_LIGHT_GRAY, 0, y, width, y); if (y != center_y) { draw_text(to_string((center_y - y) / GRID_SPACING), COLOR_BLACK, center_x + 5, y - 10); } }
draw_line(COLOR_BLACK, 0, center_y, width, center_y); // x-axis draw_line(COLOR_BLACK, center_x, 0, center_x, height); // y-axis draw_text("0", COLOR_BLACK, center_x + 5, center_y + 15);}
// Function to draw a vectorvoid draw_vector(point_2d start, vector_2d v, color c, string label, int x_offset, int y_offset){ point_2d end = {start.x + v.x, start.y + v.y}; // Adjust for Cartesian coordinates: y increases downwards draw_line(c, start.x + screen_width() / 2, screen_height() / 2 - start.y, // Convert Cartesian coordinates to screen coordinates end.x + screen_width() / 2, screen_height() / 2 - end.y); // Convert Cartesian coordinates to screen coordinates draw_text(label, c, end.x + screen_width() / 2 + x_offset, screen_height() / 2 - end.y + y_offset); // Convert Cartesian coordinates to screen coordinates}
int main(){ open_window("Vector Point to Point Example", 800, 600);
point_2d ship_position = {-50, 50}; // Ship starts at (-50, 50) point_2d island_position = {200, 250}; // Island at (200, 250)
// Calculate vectors vector_2d current_vector = {100, 5}; // Current affecting the ship vector_2d target_vector = vector_point_to_point(ship_position, island_position); vector_2d required_vector = vector_subtract(target_vector, current_vector);
while (!window_close_requested("Vector Point to Point Example")) { process_events(); clear_screen(COLOR_WHITE); draw_cartesian_grid();
// Draw island (target) draw_circle(COLOR_RED, island_position.x + screen_width() / 2, screen_height() / 2 - island_position.y, 10); draw_text("Island", COLOR_BLACK, island_position.x + screen_width() / 2, screen_height() / 2 - island_position.y - 20);
// Draw ship draw_circle(COLOR_BLUE, ship_position.x + screen_width() / 2, screen_height() / 2 - ship_position.y, 10); draw_text("Ship", COLOR_BLACK, ship_position.x + screen_width() / 2, screen_height() / 2 - ship_position.y - 20);
// Draw vectors draw_vector(ship_position, current_vector, COLOR_RED, "Current Vector", 10, -10); draw_vector(ship_position, target_vector, COLOR_GREEN, "Target Vector", 15, 15); draw_vector(ship_position, required_vector, COLOR_BLUE, "Required Vector", -50, -20);
refresh_screen(60); }
close_window("Vector Point to Point Example"); return 0;}using System;using SplashKitSDK;
public class Program{ const int GRID_SPACING = 50;
// Function to draw the Cartesian grid public static void DrawCartesianGrid() { int width = SplashKit.ScreenWidth(); int height = SplashKit.ScreenHeight(); int centerX = width / 2; int centerY = height / 2;
for (int x = 0; x <= width; x += GRID_SPACING) { SplashKit.DrawLine(Color.LightGray, x, 0, x, height); if (x != centerX) { SplashKit.DrawText(((x - centerX) / GRID_SPACING).ToString(), Color.Black, x + 2, centerY + 5); } }
for (int y = 0; y <= height; y += GRID_SPACING) { SplashKit.DrawLine(Color.LightGray, 0, y, width, y); if (y != centerY) { SplashKit.DrawText(((centerY - y) / GRID_SPACING).ToString(), Color.Black, centerX + 5, y - 10); } }
SplashKit.DrawLine(Color.Black, 0, centerY, width, centerY); // x-axis SplashKit.DrawLine(Color.Black, centerX, 0, centerX, height); // y-axis SplashKit.DrawText("0", Color.Black, centerX + 5, centerY + 15); }
// Function to draw a vector public static void DrawVector(Point2D start, Vector2D v, Color c, string label, int xOffset, int yOffset) { Point2D end = new Point2D() { X = start.X + v.X, Y = start.Y + v.Y };
SplashKit.DrawLine( c, start.X + SplashKit.ScreenWidth() / 2, SplashKit.ScreenHeight() / 2 - start.Y, end.X + SplashKit.ScreenWidth() / 2, SplashKit.ScreenHeight() / 2 - end.Y );
SplashKit.DrawText( label, c, end.X + SplashKit.ScreenWidth() / 2 + xOffset, SplashKit.ScreenHeight() / 2 - end.Y + yOffset ); }
public static void Main() { Window window = SplashKit.OpenWindow("Vector Point to Point Example", 800, 600);
Point2D shipPosition = new Point2D() { X = -50, Y = 50 }; // Ship starts at (-50, 50) Point2D islandPosition = new Point2D() { X = 200, Y = 250 }; // Island at (200, 250)
// Calculate vectors Vector2D currentVector = new Vector2D() { X = 100, Y = 5 }; // Current affecting the ship Vector2D targetVector = SplashKit.VectorPointToPoint(shipPosition, islandPosition); Vector2D requiredVector = SplashKit.VectorSubtract(targetVector, currentVector);
while (!SplashKit.WindowCloseRequested("Vector Point to Point Example")) { SplashKit.ProcessEvents(); SplashKit.ClearScreen(Color.White); DrawCartesianGrid();
// Draw island (target) SplashKit.DrawCircle(Color.Red, islandPosition.X + SplashKit.ScreenWidth() / 2, SplashKit.ScreenHeight() / 2 - islandPosition.Y, 10); SplashKit.DrawText("Island", Color.Black, islandPosition.X + SplashKit.ScreenWidth() / 2, SplashKit.ScreenHeight() / 2 - islandPosition.Y - 20);
// Draw ship SplashKit.DrawCircle(Color.Blue, shipPosition.X + SplashKit.ScreenWidth() / 2, SplashKit.ScreenHeight() / 2 - shipPosition.Y, 10); SplashKit.DrawText("Ship", Color.Black, shipPosition.X + SplashKit.ScreenWidth() / 2, SplashKit.ScreenHeight() / 2 - shipPosition.Y - 20);
// Draw vectors DrawVector(shipPosition, currentVector, Color.Red, "Current Vector", 10, -10); DrawVector(shipPosition, targetVector, Color.Green, "Target Vector", 15, 15); DrawVector(shipPosition, requiredVector, Color.Blue, "Required Vector", -50, -20);
SplashKit.RefreshScreen(60); } window.Close(); }}Vector Multiplication
Section titled “Vector Multiplication”For example, if you have a vector v1 = {2, 3} and you multiply it by a scalar s = 2, the resulting vector would be {4, 6}.
vector_multiply is particularly useful in scenarios where you need to adjust the magnitude of a vector without changing its direction. For example, when developing games, you might want to control the speed of an object by scaling its velocity vector. If an object needs to move faster or slower, multiplying its velocity vector by a scalar can achieve this.
Scenario: Spaceship Afterburners
Section titled “Scenario: Spaceship Afterburners”In a space game, if you want to double the speed of your spaceship by activating the afterburners, you can use the vector_multiply function to scale the velocity vector representing the spaceship’s movement:
const double SHIP_SPEED = 25.0; // Normal speed of the shipconst double AFTERBURNER_MULTIPLIER = 2.0; // Afterburner multiplier
vector_2d normal_velocity = { SHIP_SPEED, 0 }; // Normal velocity vector (moving right)
// Use vector_multiply to double the speed for afterburnersvector_2d afterburner_velocity = vector_multiply(normal_velocity, AFTERBURNER_MULTIPLIER);public const double SHIP_SPEED = 25.0; // Normal speed of the shippublic const double AFTERBURNER_MULTIPLIER = 2.0; // Afterburner multiplier
Vector2D normalVelocity = new Vector2D { X = SHIP_SPEED, Y = 0 }; // Normal velocity vector (moving right)
// Use VectorMultiply to double the speed for afterburnersVector2D afterburnerVelocity = SplashKit.VectorMultiply(normalVelocity, AFTERBURNER_MULTIPLIER);SHIP_SPEED: Defines the normal speed of the ship, set to25.0units per frame.AFTERBURNER_MULTIPLIER: Represents the factor by which the speed is increased when afterburners are activated. In this case, it is2.0, meaning the speed will be doubled.normal_velocity: The ship moves to the right with a speed of25.0units and no vertical movement.afterburner_velocity: This vector is calculated by multiplying thenormal_velocityvector by theAFTERBURNER_MULTIPLIER. Thevector_multiplyfunction scales the velocity, effectively doubling the speed of the ship when the afterburners are activated.

Use this code in your own IDE to play with the functions for yourself!
#include "splashkit.h"
using std::to_string;
// Define constantsconst int GRID_SPACING = 50;const double NORMAL_SHIP_VELOCITY = 25.0; // Normal speed of the shipconst double AFTERBURNER_MULTIPLIER = 2.0; // Afterburner multiplier
// Function to draw the cartesian gridvoid draw_cartesian_grid(){ for (int x = 0; x < screen_width(); x += GRID_SPACING) { draw_line(COLOR_LIGHT_GRAY, x, 0, x, screen_height()); if (x != screen_width() / 2) { draw_text(to_string(x - screen_width() / 2), COLOR_BLACK, x, screen_height() / 2 + 5); } }
for (int y = 0; y < screen_height(); y += GRID_SPACING) { draw_line(COLOR_LIGHT_GRAY, 0, y, screen_width(), y); if (y != screen_height() / 2) { draw_text(to_string(screen_height() / 2 - y), COLOR_BLACK, screen_width() / 2 + 5, y); } }
draw_line(COLOR_BLACK, 0, screen_height() / 2, screen_width(), screen_height() / 2); // x-axis draw_line(COLOR_BLACK, screen_width() / 2, 0, screen_width() / 2, screen_height()); // y-axis draw_text("0", COLOR_BLACK, screen_width() / 2 + 5, screen_height() / 2 + 5);}
// Function to draw a vectorvoid draw_vector(vector_2d start, vector_2d end, color c, std::string label, int x_offset, int y_offset){ draw_line(c, start.x + screen_width() / 2, screen_height() / 2 - start.y, end.x + screen_width() / 2, screen_height() / 2 - end.y); draw_text(label, c, end.x + screen_width() / 2 + x_offset, screen_height() / 2 - end.y + y_offset);}
int main(){ open_window("Ship with Velocity Vector", 800, 600);
vector_2d ship_position = { -300, 50 }; // Ship starts at (-300, 50) vector_2d velocity = { NORMAL_SHIP_VELOCITY, 0 }; // Normal velocity vector (moving right) bool afterburners_activated = false; // Flag to track afterburner activation
while (!window_close_requested("Ship with Velocity Vector")) { process_events(); clear_screen(COLOR_WHITE); draw_cartesian_grid();
// Check if the ship has crossed the y-axis if (ship_position.x >= 0) { if (!afterburners_activated) { // Activate afterburners (double the speed) velocity = vector_multiply(velocity, AFTERBURNER_MULTIPLIER); afterburners_activated = true; // Set flag to true } }
// Update ship position based on velocity ship_position.x += velocity.x; // Move ship according to the velocity
// Draw ship draw_circle(COLOR_BLUE, ship_position.x + screen_width() / 2, screen_height() / 2 - ship_position.y, 10); draw_text("Ship", COLOR_BLACK, ship_position.x + screen_width() / 2, screen_height() / 2 - ship_position.y - 20);
// Draw velocity vector draw_vector(ship_position, { ship_position.x + velocity.x, ship_position.y + velocity.y }, COLOR_RED, "Velocity", 10, -10);
// Display the magnitude of the velocity vector at the top left draw_text("Velocity Magnitude: " + to_string(vector_magnitude(velocity)), COLOR_BLACK, 10, 10);
// Display message if afterburners are activated if (afterburners_activated) { draw_text("AFTERBURNERS ACTIVATED", COLOR_GREEN, ship_position.x + screen_width() / 2 - 10, ship_position.y + screen_height() / 2 + 20); }
delay(200);
refresh_screen(60); }
close_window("Ship with Velocity Vector"); return 0;}using System;using SplashKitSDK;
// Define constantsconst int GRID_SPACING = 50;const double NORMAL_SHIP_VELOCITY = 25.0; // Normal speed of the shipconst double AFTERBURNER_MULTIPLIER = 2.0; // Afterburner multiplier
// Function to draw the Cartesian gridvoid DrawCartesianGrid(){ int screenWidth = SplashKit.ScreenWidth(); int screenHeight = SplashKit.ScreenHeight(); int centerX = screenWidth / 2; int centerY = screenHeight / 2;
for (int x = 0; x < screenWidth; x += GRID_SPACING) { SplashKit.DrawLine(Color.LightGray, x, 0, x, screenHeight); if (x != centerX) { SplashKit.DrawText(((x - centerX)).ToString(), Color.Black, x, centerY + 5); } }
for (int y = 0; y < screenHeight; y += GRID_SPACING) { SplashKit.DrawLine(Color.LightGray, 0, y, screenWidth, y); if (y != centerY) { SplashKit.DrawText(((centerY - y)).ToString(), Color.Black, centerX + 5, y); } }
SplashKit.DrawLine(Color.Black, 0, centerY, screenWidth, centerY); // x-axis SplashKit.DrawLine(Color.Black, centerX, 0, centerX, screenHeight); // y-axis SplashKit.DrawText("0", Color.Black, centerX + 5, centerY + 5);}
// Function to draw a vectorvoid DrawVector(Vector2D start, Vector2D end, Color c, string label, int xOffset, int yOffset){ SplashKit.DrawLine(c, start.X + SplashKit.ScreenWidth() / 2, SplashKit.ScreenHeight() / 2 - start.Y, end.X + SplashKit.ScreenWidth() / 2, SplashKit.ScreenHeight() / 2 - end.Y); SplashKit.DrawText(label, c, end.X + SplashKit.ScreenWidth() / 2 + xOffset, SplashKit.ScreenHeight() / 2 - end.Y + yOffset);}
SplashKit.OpenWindow("Ship with Velocity Vector", 800, 600);
Vector2D shipPosition = new Vector2D() { X = -300, Y = 50 }; // Ship starts at (-300, 50)Vector2D velocity = new Vector2D() { X = NORMAL_SHIP_VELOCITY, Y = 0 }; // Normal velocity vector (moving right)bool afterburnersActivated = false; // Flag to track afterburner activation
while (!SplashKit.WindowCloseRequested("Ship with Velocity Vector")){ SplashKit.ProcessEvents(); SplashKit.ClearScreen(Color.White); DrawCartesianGrid();
// Check if the ship has crossed the y-axis if (shipPosition.X >= 0) { if (!afterburnersActivated) { // Activate afterburners (double the speed) velocity = SplashKit.VectorMultiply(velocity, AFTERBURNER_MULTIPLIER); afterburnersActivated = true; // Set flag to true } }
// Update ship position based on velocity shipPosition = SplashKit.VectorAdd(shipPosition, velocity); // Move ship according to the velocity
// Draw ship SplashKit.DrawCircle(Color.Blue, shipPosition.X + SplashKit.ScreenWidth() / 2, SplashKit.ScreenHeight() / 2 - shipPosition.Y, 10); SplashKit.DrawText("Ship", Color.Black, shipPosition.X + SplashKit.ScreenWidth() / 2, SplashKit.ScreenHeight() / 2 - shipPosition.Y - 20);
// Draw velocity vector DrawVector(shipPosition, SplashKit.VectorAdd(shipPosition, velocity), Color.Red, "Velocity", 10, -10);
// Display the magnitude of the velocity vector at the top left SplashKit.DrawText("Velocity Magnitude: " + SplashKit.VectorMagnitude(velocity).ToString("F2"), Color.Black, 10, 10);
// Display message if afterburners are activated if (afterburnersActivated) { SplashKit.DrawText("AFTERBURNERS ACTIVATED", Color.Green, shipPosition.X + SplashKit.ScreenWidth() / 2 - 10, shipPosition.Y + SplashKit.ScreenHeight() / 2 + 20); }
SplashKit.Delay(200); SplashKit.RefreshScreen();}Conclusion
Section titled “Conclusion”Here we have explored some simple vector arithmetic operations, including vector addition, subtraction, and multiplication. These fundamental operations are useful in various programming scenarios, particularly in game development. By understanding and applying vector arithmetic, you can effectively calculate and manipulate directions, positions, and forces, enhancing your ability to create realistic and dynamic movements.
Mastering vector arithmetic will empower you to build more complex and interactive systems, laying a solid foundation for advanced topics in physics and game development.